高考数学一直是学生们备战的重要科目之一,其中求最小值问题更是常考不衰,本文将介绍一种利用均值不等式秒杀高考数学中最小值问题的方法,帮助考生快速准确地解答此类题目,提高解题效率。
均值不等式概述
均值不等式是数学中一种重要的不等式,用于处理一些涉及平均值的问题,其基本形式为:对于任意的正数a、b,都有a+b≥2√ab(当且仅当a=b时等号成立),这个不等式可以帮助我们快速找到某些表达式的最小值。
长沙市高考数学题中的最小值问题
在长沙市高考数学试题中,求最小值问题常常出现在函数、几何、代数等多个领域,这些问题需要学生掌握一定的数学知识和解题技巧,以便快速找到最小值,下面我们将通过一道典型的高考数学题来展示如何利用均值不等式求解最小值问题。
例题:已知函数f(x)=x^2+(k/x),其中k为常数,求f(x)的最小值。
分析:这道题目考察的是二次函数和均值不等式的综合运用,我们可以先将函数f(x)进行变形,然后利用均值不等式求解。
利用均值不等式求解最小值问题
针对上述例题,我们可以按照以下步骤求解:
1、函数变形:将函数f(x)=x^2+(k/x)进行变形,得到f(x)=x^2+(k/x)+[(k/x)*x],即f(x)=x^2+k/x+k,这一步的目的是为了将函数转化为适合应用均值不等式的形式。
2、应用均值不等式:对于变形后的函数f(x)=x^2+k/x+k,我们可以利用均值不等式进行求解,根据均值不等式,我们知道a+b≥2√ab,所以对于f(x)中的每一项都可以应用这个不等式,特别地,对于k/x和x这两项,我们有k/x+x≥2√(k/x*x),即k/x+x≥2√k,将这个不等式代入到f(x)中,我们得到f(x)≥x^2+2√k,这说明函数f(x)的最小值不小于x^2+2√k。
3、求解等号成立条件:根据均值不等式的性质,我们知道等号成立的条件是a=b,即k/x=x,解这个方程我们可以得到x=√k,这意味着当x=√k时,函数f(x)取得最小值,此时的最小值为f(x)=2√k,函数f(x)的最小值为2√k。
其他应用实例及注意事项
除了上述例题外,均值不等式在求解其他类型的高考数学题中的最小值问题也有广泛应用,在几何题中,我们可以通过均值不等式找到线段长度的最小值;在代数题中,我们可以利用均值不等式求解表达式的最小值等,在应用均值不等式求解最小值问题时,需要注意以下几点:一是要确保等号成立的条件得到满足;二是要注意题目中可能存在的约束条件;三是要结合题目特点灵活运用均值不等式。
本文介绍了利用均值不等式秒杀高考数学中最小值问题的方法,通过一道典型的高考数学题为例,详细阐述了如何利用均值不等式求解最小值问题,还介绍了均值不等式在其他领域的应用及注意事项,希望本文能对广大高考生备考数学科目有所帮助,未来随着高考数学试题的不断创新和发展,我们将继续关注均值不等式在求解最小值问题中的应用,并探索更多高效的解题方法。


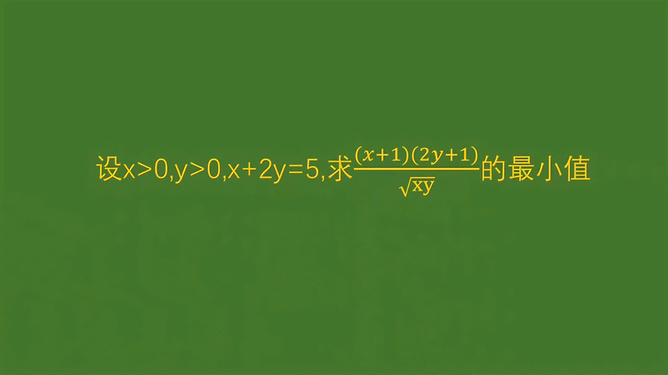












 京公网安备11000000000001号
京公网安备11000000000001号 京ICP备11000001号
京ICP备11000001号
还没有评论,来说两句吧...